Seit 1998 haben die allerbesten Teilnehmer am Känguruwettbewerb aus den Klassenstufen 9 bis 13 Einladungen zu internationalen Mathe-Camps erhalten. Solche Camps finden in mehreren Ländern statt. Wir beteiligen uns regelmäßig an dem Camp in Zakopane (Polen) und veranstalten jedes Jahr ein Camp am Werbellinsee bei Berlin.
Jedes Jahr lädt unser Verein die besten Teilnehmenden der Klassen 9 und 10 des Känguru-Wettbewerbs aus den Niederlanden, Österreich, Polen, der Schweiz, der Slowakei, Tschechien, Ungarn und natürlich Deutschland an den Werbellinsee nördlich von Berlin ein. In der idyllisch gelegenen Anlage am See besuchen die Jugendlichen am Vormittag Workshops zu spannenden mathematischen Themen wie dem Erzeugen von optischen Illusionen oder der Strategiefindung für Spiele. Am Nachmittag finden sportliche Wettkämpfe statt und wir erkunden die Gegend, traditionell das Schiffshebewerk in Niederfinow und die Naturtherme in Templin. Zudem finden mit Speed- und Teamwettbewerb herausfordernde mathematische Wettstreite statt. Als Highlight der Woche geht es zum Bergfest nach Berlin. Dort werden das Spektrum im Technikmuseum oder die Kuppel des Reichstags besucht, und es ist Zeit für Entdeckungen auf eigene Faust.
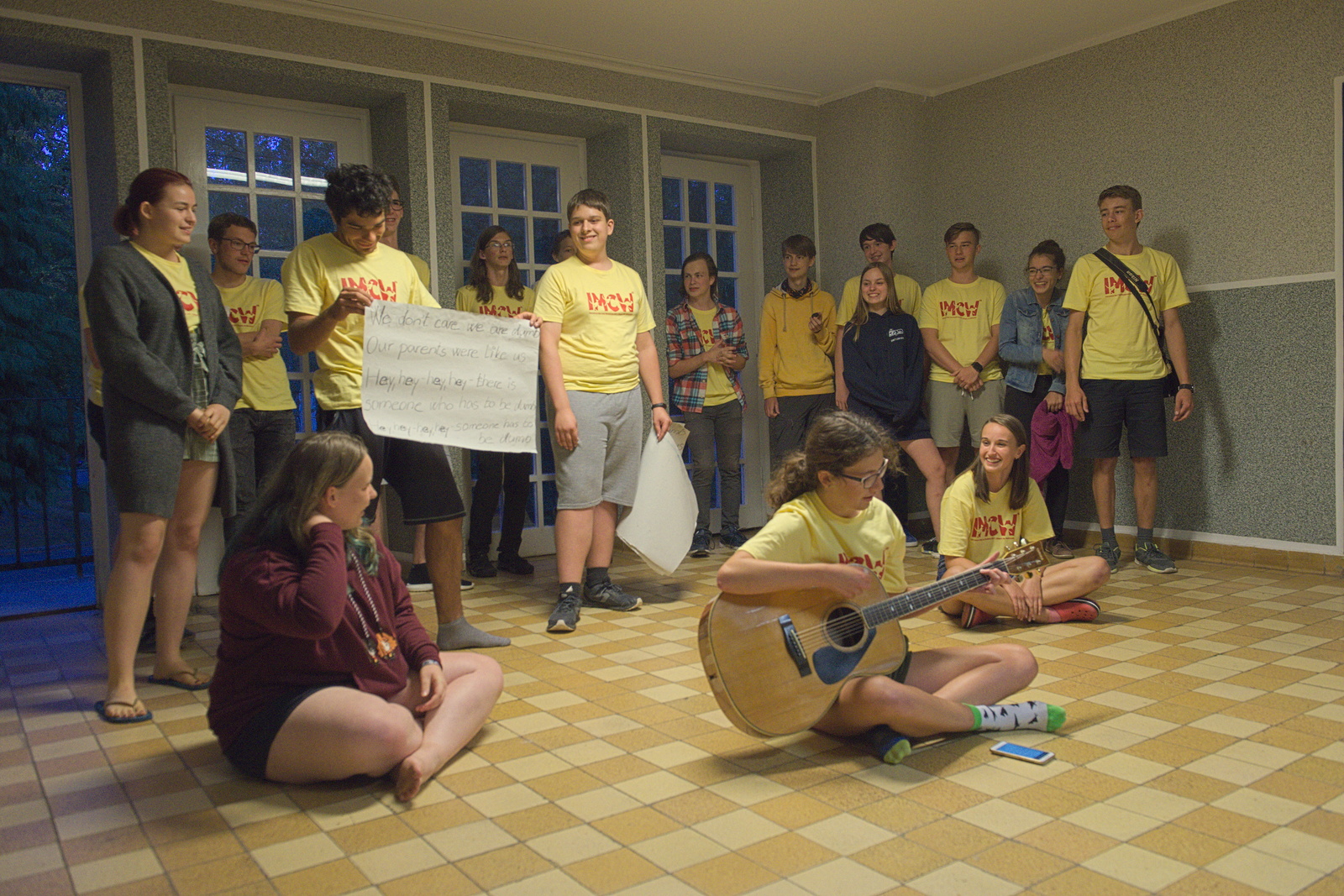
Eine zweite Gruppe der allerbesten Teilnehmenden der Klassen 9 und 10 des Känguru-Wettbewerbs in Deutschland hat die Gelegenheit, am internationalen Mathe-Camp in Zakopane teilzunehmen. Dazu laden unsere polnischen Kollegen Teilnehmende des Känguru-Wettbewerbs aus Polen, Deutschland, Frankreich, Litauen, Belarus, der Ukraine und einigen weiteren Ländern ein. Die Unterkunft ist direkt am Fuße der Hohen Tatra gelegen, in die atemberaubende Wanderungen unternommen werden. An den Nachmittagen gibt es mathematische Workshops und Wettkämpfe, gefolgt von geselligen Abenden mit Tischtennis, Schach und Gesellschaftsspielen. Neben den Wanderungen finden als Highlights Ausflüge in das Salzbergwerk Wieliczka und die beeindruckende Großstadt Krakau statt.
Im folgenden Bericht gibt es einige Eindrücke und weitere Bilder:
Bericht über das Internationale Mathe-Sommercamp in Zakopane vom 04. bis 13.08.2016
Der Dreiländerwettbewerb DATCH — Das Känguru wurde 2011 ins Leben gerufen. Es nehmen die erfolgreichsten Mädchen und Jungen beim Känguru-Wettbewerb in den Klassenstufen 7 und 8 aus Deutschland, Österreich und der Schweiz teil. Der Wettbewerb fand bereits in Deutschland, Österreich und viele Jahre lang in Quarten in der Schweiz statt. Im Jahr 2024 hat der Wettbewerb in Wien stattgefunden, in Zusammenarbeit mit dem Projekt Mathematik macht Freude der Universität Wien.
In drei mathematischen Wettbewerben stellen die Teilnehmer ihr Können unter Beweis. Der Känguru-Speedwettbewerb findet mit nach Ländern gemischten Teams statt und es werden Teamfähigkeit und Schnelligkeit gefordert. Beim Einzelwettbewerb steht das exakte Begründen gefundener Lösungen im Mittelpunkt. Und beim Gruppenwettbewerb kommt es auf die richtige Strategie und eine anschauliche Präsentation einer Lösung an.
Das Land mit den meisten Punkten beim Gruppenwettbewerb gewinnt neben Sachpreisen den Wanderpokal, der zwischen den Schulen der Teilnehmer wandert. 2024 ging der Pokal an Deutschland.
Außerdem bleibt Zeit für Exkursionen, um die Stadt Wien kennenzulernen.
Wir falten ein rechteckiges Stück Papier fünf Mal, wobei sich bei jedem Schritt die Größe halbiert und bei jedem Schritt die Richtung des Faltens geändert wird. Danach schneiden wir die vier Ecken ab. Jetzt falten wir das Papier wieder auseinander. Wie viele Löcher hat das aufgefaltete Papier?
(A) 1 (B) 9 (C) 12 (D) 16 (E) 21
Gegeben ist das Quadrat ABCD. Der Punkt X liegt auf der Seite AB (X≠A, X≠B) und ist Mittelpunkt eines Kreises, dessen Radius gleich lang ist wie die Seite des Quadrates. U, V und W sind die drei Punkte, die jeweils sowohl auf einer Quadratseite als auch auf diesem Kreis liegen. Begründe, wieso die Fläche des Vierecks XUVW exakt halb so groß ist wie jene des gegebenen Quadrates, unabhängig von der Lage von X.
Im Morsealphabet sind alle Buchstaben mit Hilfe der zwei Zeichen · und – codiert. Für die Buchstaben A, B, C, D, E gilt zum Beispiel:
A = ·– B = –··· C = –·–· D = –·· E = ·
Werden Buchstabenfolgen ohne Abstand codiert, lassen sie sich in einigen Fällen nicht eindeutig decodieren, wenn sie von links nach rechts gelesen werden. Beispielsweise kann die Zeichenfolge ·–·· sowohl ED als auch AEE bedeuten.
a) Findet mit den Zeichen · und – eine Codierung für A bis E, die für jeden der Buchstaben höchstens so viele Zeichen verwendet wie das Morsealphabet (also höchstens zwei Zeichen für A, höchstens vier für B,...), mit der sich aber jede codierte Buchstabenfolge eindeutig decodieren lässt.
b) Lässt sich die in a) gefundene Codierung durch eine Codierung für den Buchstaben F mit höchstens vier Zeichen erweitern, so dass sich wiederum jede codierte Buchstabenfolge eindeutig decodieren lässt?
